4D reconstruction of murine developmental trajectories using spherical harmonics
Developmental Cell 1st September 2022
10.1016/j.devcel.2022.08.005
EMBL researchers use a “fearless” computer reconstruction and a two-centuries-old mathematical approach to study limb bud growth
Grasping hands with five fingers and opposable thumbs represented a key step in primate evolution. For our ancestors, it was a key adaptation to life in the trees.
However, when our hands first develop in the womb, they form amorphous buds without distinct fingers. How the human hand grows from a compact bud to a structure with five independent fingers is not yet clearly understood. So far, we do not have the technology to continuously image how our limbs grow in the womb and researchers base their study of this developmental process on observing it at individual time points.
Now, Giovanni Dalmasso, postdoc in the Sharpe Group at EMBL Barcelona, has brought the field a step closer to a more complete vision of how our hands develop. His latest project FeARlesS (First Accurate descRiption of Limb Shape) has been published in Developmental Cell.
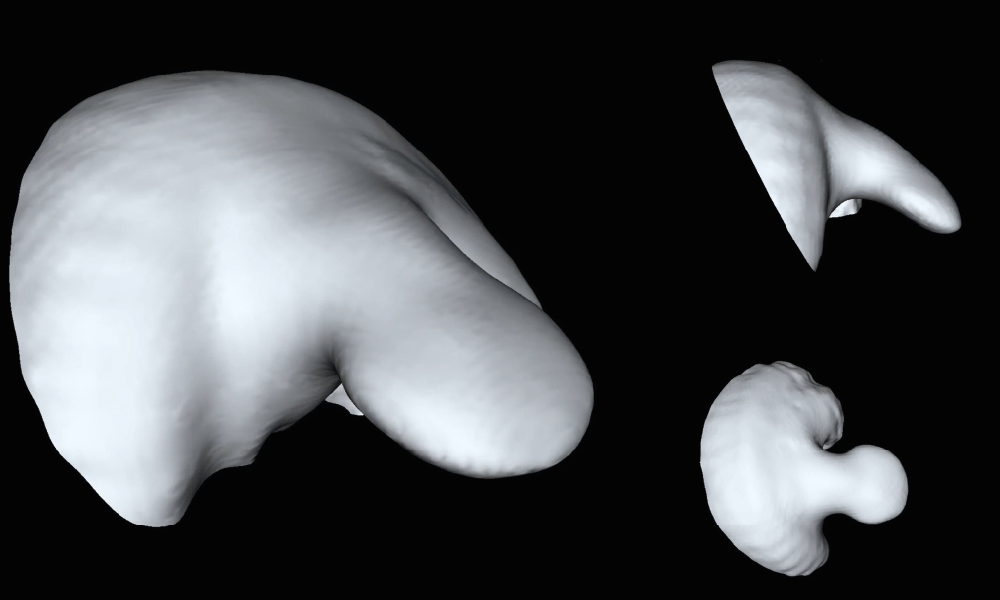
“My project aims to create a computer reconstruction of an ideal limb,” explained Dalmasso. “That means it allows us to recreate the ideal full development of the hand without time gaps.” His computational approach aims to recreate the continuous evolution in time and space of the developmental stages of limbs, based on 3D volumetric images.
So, how does one create a model of continuous development when the available experimental data does not cover all intervening time points? According to Dalmasso, it has not been an easy path. “We tried several mathematical approaches. Among others, we used principal component analysis and interpolation, but they were not working. Together with my colleague Marco Musy, we decided to give spherical harmonics a try.”
Spherical harmonics is an old mathematical approach that dates back to 1782. It was invented by Pierre Simon de Laplace and is fundamental to many theoretical and practical applications, like calculating the gravitational fields of planets. To be able to apply this model to studying limb development, Dalmasso had to map the 3D structure of the limb into a sphere. This eventually allowed him to represent each limb using spherical harmonic functions.
One key feature of these functions is that they are based on coefficients, mathematical terms that provide precision. To represent limbs with spherical harmonics, the limb shapes are transformed into a set of points that are easier to handle. After that, the set of points needs to be reconverted to the limb shape. For this transition, the more coefficients one uses, the more accurate the limb’s representation becomes.
“The experimental data that we had access to did not cover all time points during development and had intrinsic errors, so we needed to calculate the coefficients for those time points that are missing,” explained Dalmasso. “Spherical Harmonics allows us to reduce the complexity of the problem, helping us create a smooth reconstruction and be a bit closer to creating an ideal limb.”
In order to validate the model, the researchers also applied this method to understanding the development of another organ, the heart. The spherical-harmonics based method also worked on this more complex structure. However, to get to the visualisation of the development of a complete heart, more experimental data would be needed.
This study represents an important step towards achieving an accurate computer simulation of the development of an entire embryo. This could potentially help scientists better understand developmental defects and congenital diseases in the future.
Developmental Cell 1st September 2022
10.1016/j.devcel.2022.08.005